Given two obstacles, make the robot go around the first one and stops 3 cm behind the second one for 10 seconds and finally come back, as in Figure 1.
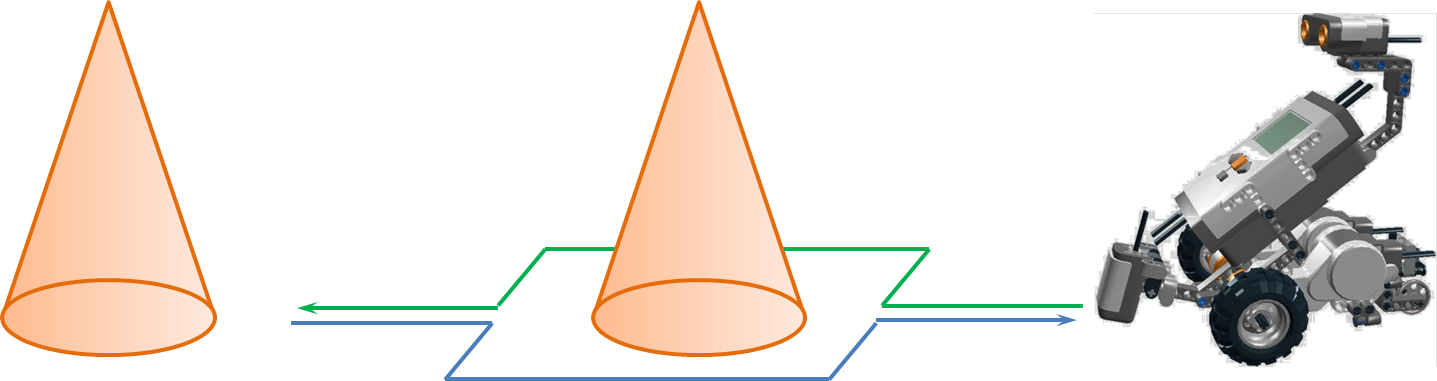
At the end of the experience...
Objectives
- Make the robot reach the second obstacle
- Go back to the starting position
- Understand the basic ROS concepts (launcher, compiler and publisher/subscriber)
- Use the gyroscope to improve the robot performances
Plus
- Use the thrid engine to move the ultrasonic sensor
- Object Oriented (OO) approach
Challenges
- Unknow distance between the two obstacles
What we want
- Code (BitBucket)
- Video (YouTube or BitBucket)
- Report (PDF using BitBucket) containing
- The algorithm overview
- The procedures to make the robot go straight and turn
- What are the main robot problems and why
- The Launcher description
- The CMakeLists.txt description
Explanation
Preliminary steps
cd ~/Workspace/ros/catkin_ws/src git clone https://<your_bb_username>@bitbucket.org/iaslab-unipd/nxt.git cd ..
catkin_make --force-cmake -G"Eclipse CDT4 - Unix Makefiles" roslaunch nxt_unipd nxt_lab.launch roslaunch nxt_unipd teleop_keyboard.launch
Robot configuration
nxt_lab.yaml
- type: ultrasonic
frame_id: ultrasonic_link
name: ultrasonic_sensor
port: PORT_4
spread_angle: 0.2
min_range: 0.01
max_range: 2.5
desired_frequency: 5.0
Program launcher
nxt_lab.launch
<group ns="base_parameters">
<param name="r_wheel_joint" value="r_wheel_joint"/>
<param name="l_wheel_joint" value="l_wheel_joint"/>
<param name="wheel_radius" value="0.022"/>
<param name="wheel_basis" value="0.055"/>
<param name="vel_to_eff" value="0.2"/>
<param name="l_vel_to_eff" value="0.1"/>
<param name="r_vel_to_eff" value="0.1"/>
</group>
Robot controller
advanced_control.py
\[v_{trans}^{est} \left[i+1\right] = \frac{1}{2} \left( v_{trans}^{est}\left[i\right] + \frac{1}{2} \left( v_{rot}^{reg}\left[i,j_{wheel}^{l} \right] + v_{rot}^{reg}\left[i,j_{wheel}^{r} \right] \right) r_{wheel} \right)\]
\[v_{rot}^{est} \left[i+1\right] = \frac{1}{2} \left( v_{rot}^{est}\left[i\right] + \frac{1}{2} \left( v_{rot}^{reg}\left[i,j_{wheel}^{l} \right] - v_{rot}^{reg}\left[i,j_{wheel}^{r} \right] \right) \frac{r_{wheel}}{b_{wheel}} \right)\]
where:
\(v_{trans}^{est} \left[i\right]\) is the estimated translational velocity at the instant \(i\)
\(v_{rot}^{est} \left[i\right]\) is the estimated rotational velocity at the instant \(i\)
\(v_{rot}^{reg}\left[i,j_{wheel}^{l} \right]\) is the registered rotational velocity for the joint of the left wheel at the instant \(i\)
\(v_{rot}^{reg}\left[i,j_{wheel}^{r} \right]\) is the registered rotational velocity for the joint of the right wheel at the instant \(i\)
\(r_{wheel}\) is the wheel radius
\(b_{wheel}\) is the wheel basis
\[v_{trans}^{cmd} \left[i+1\right] = v_{trans}^{des}\left[i\right] + k_{trans} \left( v_{trans}^{des}\left[i \right] - v_{trans}^{est}\left[i +1 \right] \right)\]
\[v_{rot}^{cmd} \left[i+1\right] = v_{rot}^{des}\left[i\right] + k_{rot} \left( v_{rot}^{des}\left[i \right] - v_{rot}^{est}\left[i \right] \right)\]
where:
\(v_{trans}^{cmd} \left[i\right]\) is the translational velocity applied to the joint at the instant \(i\)
\(v_{rot}^{cmd} \left[i\right]\) is the rotational velocity applied to the joint at the instant \(i\)
\(v_{trans}^{des}\left[i \right]\) is the desired transational velocity for the joint at the instant \(i\)
\(v_{rot}^{des}\left[i \right]\) is the desired rotational velocity for the joint at the instant \(i\)
\(k_{trans}\) is the trasational constant
\(k_{rot}\) is the rotational constant
\[F \left[i+1\right] = k_v^F \left( v_{trans}^{cmd}\left[i + 1\right] \frac{1}{r_{wheel}} - v_{rot}^{cmd}\left[i +1 \right] \frac{b_wheel}{r_{wheel}} \right)\]
where:
\(F \left[i\right]\) is the effort applied to the joint at the instant \(i\)
\(k_v^F\) is the constant to transform velocity to effort
Robot teleoperation
nxt_key.cpp
switch(c)
{
case KEYCODE_L:
ROS_DEBUG("LEFT");
angular_ = 2.0;
break;
case KEYCODE_R:
ROS_DEBUG("RIGHT");
angular_ = -2.0;
break;
case KEYCODE_U:
ROS_DEBUG("UP");
linear_ = 0.15;
break;
case KEYCODE_D:
ROS_DEBUG("DOWN");
linear_ = -0.15;
break;
}
teleop_keyboard.launch
<node pkg="nxt_unipd" type="nxt_teleop_key" name="nxt_teleop_key" output="screen"> <param name="scale_linear" value="1" type="double"/> <param name="scale_angular" value="1" type="double"/> </node>
Sensors messages
Header header float64 range float64 range_min float64 range_max float64 spread_angle